Interpretación de histogramas

Los histogramas nos pueden brindar mucha información que en las empresas ni se imaginan.

Para una persona que conozca un proceso cualquiera, la forma que tiene  un histograma construido a partir de una muestra de datos extraídos de dicho proceso, le indicará qué podría estar ocurriendo con su proceso.

A continuación se muestran los distintos tipos de histogramas que se podrían encontrar, con una interpretación de lo que probablemente esté ocurriendo.

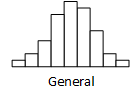
Histograma general: la media del histograma está en el centro del rango de datos. La frecuencia es mayor en el centro y disminuye gradualmente hacia los extremos, ajustándose a una distribución normal. Se presenta en casi todos los casos en que se representa una medida importante en un proceso productivo.

Histograma con sesgo positivo o negativo: tiene forma asimétrica. La media del histograma está a la izquierda (o a la derecha) y la frecuencia disminuye lentamente hacia la derecha (o hacia la izquierda). Se presenta cuando el límite inferior (o el superior) se controla teóricamente o por un valor de especificación; o también cuando no se presentan valores inferiores (o superiores) a cierto límite.

Histograma con precipicio: es similar al tipo con sesgo; pero con un descenso más brusco hacia un lado. Este tipo se presenta frecuentemente cuando se ha hecho una inspección al 100% y se han separado elementos que no cumplen con el límite inferior (o superior) de especificación del producto.

Histograma multimodal: hace zigzag sobre la forma general. Se presenta cuando no se ha elegido correctamente la longitud de clase y el número de clases, ya sea porque el número de datos no es suficiente grande para trazar el histograma (n < 50) o porque se han considerado muchas clases para el número de datos que hay.

Histograma bimodal: se ven dos histogramas generales. Se presenta cuando se mezclan dos distribuciones con medias muy diferentes; por ejemplo, cuando en el proceso hay dos turnos, o dos máquinas, o dos operarios, etc. que trabajan de manera distinta.

Histograma con pico aislado: hay un pequeño pico, que está aislado de un histograma de tipo general. Se presenta cuando se incluye una pequeña cantidad de datos con una distribución diferente, ya sea por una anormalidad en el proceso, por error de medición o por inclusión de datos de otro proceso.

Histograma planicie: las frecuencias forman una planicie. Se presenta cuando se mezclan varios histogramas que tienen medias diferentes y distribuciones diferentes, de tal manera que el conjunto forma una planicie.

Casos de aplicación

Caso 1:

Una empresa de manufactura recibe componentes de un proveedor, a quien se le ha indicado que debe cumplir unas especificaciones: límite de especificación inferior (LEi) y límite de especificación superior (LEs). Uno de los empleados se encarga de medir aleatoriamente algunos componentes, sin registrar los datos; pero se ha dado cuenta de que hay datos cercanos al LEi,  pero lejanos al LEs. Ante esto, ¿qué recomendaría usted?

Respuesta: lo recomendable es tomar una muestra de los componentes, medirlos y construir un histograma. A continuación se muestra el histograma resultante:

¿Qué se podría concluir?

Respuesta: Según se aprecia, el proveedor solo envía los componentes que cumplen con las especificaciones establecidas, descartando los defectuosos. Es fácil darse cuenta de que, si no hubiese separado los componentes que no cumplen con el LEi, se tendría un histograma tipo general con una media que está muy lejos del valor medio entre especificaciones. El proceso del proveedor está muy desfasado hacia la izquierda.

¿Cree usted que esto le afecta a la empresa manufacturera?

Respuesta: podría creerse que a la empresa manufacturera no le afecta, pues lo que le importa es que se cumpla con las especificaciones; pero realmente sí le afecta, pues el hecho de que haya una cantidad de componentes descartados, le va a significar una pérdida monetaria  al proveedor, y es un hecho que ese costo se lo va a cargar a la empresa manufacturera. Si el proveedor mejorase su proceso, no descartaría componentes, disminuirían sus costos, y le podría ofrecer un mejor precio a la empresa manufacturera.

Caso 2:

En un taller de carpintería se desechan trozos de madera, producto de los cortes que hacen continuamente de las planchas de madera de grandes dimensiones.

¿Qué utilidad podría tener construir un histograma a partir de una muestra de los pesos de trozos de madera desechados?

Respuesta: sería muy útil, pues mostrará cómo se distribuyen esos pesos.

¿Y cómo tendría que ser el histograma resultante si en el taller hicieran correctamente los cortes, con el propósito de desechar la menor cantidad posible de madera?

Respuesta: tendría que ser un histograma con sesgo positivo. Mientras mayor sea el sesgo, menor será la cantidad de madera que se desecha.

¿Por qué en este caso no se espera un histograma tipo general?

Respuesta: porque no se está procurando un peso promedio, sino el menor peso posible.

Caso 3:

Suponga que usted es el gerente de una empresa que fabrica discos metálicos recubiertos con plástico. El jefe de producción tiene una muestra que fue extraída durante tres días de producción. En la siguiente figura se muestra el histograma que representa dicha muestra.

¿Qué le recomendaría al jefe de producción?

Respuesta: le recomendaría que tome una muestra más grande, pues solo ha considerado 14 discos, lo que ha dado como resultado un histograma multimodal.