El 16 de mayo de 1924, Walter A.
Shewhart, un físico estadounidense, entregó un informe de una página a su jefe
en Bell Technologies, destinado
a cambiar la historia de la calidad. En él, un breve texto acompañaba a un
gráfico, hoy conocido como gráfico o carta de control. Actualmente, pese a que
sus gráficos de control siguen siendo útiles, muchos los emplean de manera
incorrecta por el desconocimiento que tienen de los fundamentos estadísticos
que los sustentan.
Los gráficos de control nos permiten visualizar cómo va
cambiando la variabilidad de una determinada medida (por ejemplo, el peso del
agua embotellada que va saliendo de un proceso de producción), a lo largo del
tiempo.
Un gráfico de control está conformado por una línea central,
que suele medir un promedio; dos límites de control, uno por encima y otro por
debajo de la línea central; y una serie de valores característicos registrados
en el gráfico que representan el estado de una medida de un proceso a lo largo
del tiempo.
La gran utilidad que tienen los gráficos de control es que permiten averiguar, en tiempo real, las causas de las variabilidades que están deformando el proceso que se está controlando, ya sea un proceso productivo o un servicio, de manera que se puedan hacer las correcciones pertinentes y mejorar el proceso continuamente.
La gran utilidad que tienen los gráficos de control es que permiten averiguar, en tiempo real, las causas de las variabilidades que están deformando el proceso que se está controlando, ya sea un proceso productivo o un servicio, de manera que se puedan hacer las correcciones pertinentes y mejorar el proceso continuamente.
Si todos los valores se encuentran dentro de los límites,
llamados “límites de control”, y no se presenta alguna situación atípica (no
aleatoria), se dice que el proceso está bajo control; en caso contrario se puede
afirmar que el proceso está fuera de control. En las Figuras 1 y 2 se
muestran estas dos situaciones.
Tipos de gráficos de control
Gráficos de control de
variables: se
aplican a características que se pueden medir. Generalmente los datos que se
utilizan provienen de una población que se puede describir con una distribución
normal.
Ventajas principales:
·
Todas las características de los procesos son
medibles.
·
Una medición proporciona más información que un
atributo.
·
Emplea muestras más pequeñas.
·
La acción correctiva es rápida.
Gráficos de control de atributos: se emplean cuando es posible
establecer la ausencia o existencia de una característica de calidad.
Generalmente se asocian con distribuciones discretas, como la binomial o
Poisson. Proporcionan menos información que los gráficos de control de
variables.
Ventajas principales:
·
Los datos por atributos existen en todos los
procesos y se pueden obtener de manera rápida y económica.
·
Un gráfico puede controlar varias
características.
·
Son fáciles de construir e interpretar.
Desventaja importante: el proceso de decisión con estos
gráficos de control es más lento.
En la siguiente tabla se presentan los tipos de gráficos de
control de variables más utilizados, y las fórmulas necesarias para determinar sus límites de control. Estas fórmulas han sido deducidas asumiendo que casi el
100% de los datos se encuentran entre el valor medio ± 3 veces la desviación estándar
correspondiente.
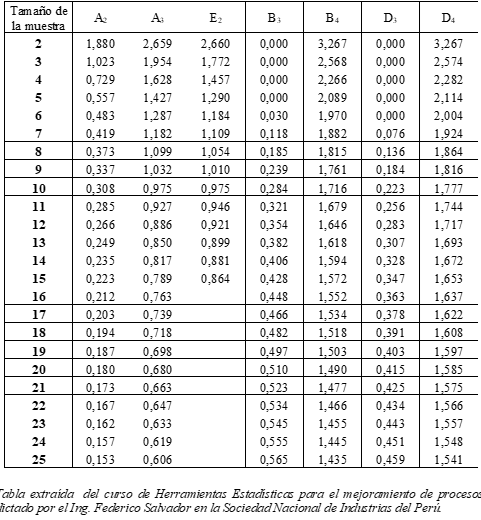
Los valores de los coeficientes
A2, A3, D3, D4, B3, B4, E2 dependen del tamaño de las muestras que se obtienen
para trazar cada punto del gráfico, y se encuentran en una tabla, al final de este artículo.
Interpretación de los gráficos de control
Para que un gráfico de control sea correctamente
interpretado, es recomendable que esté conformado por lo menos por 20 puntos.
Una vez que ya se ha instalado un gráfico de control, es
decir, una vez que ya se han determinado la línea central y los límites de
control superior e inferior, y se procede a controlar el proceso considerando
dichos límites, se podrá afirmar que el proceso está fuera de control en las siguientes
situaciones:
·
Si hay al menos un punto más
allá de los límites de control. Considerando que los datos se distribuyen normalmente, el 99,73 % de
estos estarán dentro de dichos límites de control, y solo el 0,27% se espera
que esté fuera (véase “Propiedades de la curva normal, pág. 91, libro
Estadística del mismo autor). Por lo tanto, se espera que, bajo condiciones
normales, 2,7 de cada mil puntos estén fuera de los límites de control, y,
cuando esto ocurra, lo más probable es que se deba a una causa asignable.
Se
denomina ARL (longitud promedio de
corrida), al número de puntos consecutivos que se espera que haya antes de
tener un punto fuera de los límites de control.
Entonces: ARL = 1/0,0027 =
370,37.
·
Racha: si hay 7 puntos consecutivos a
un lado de la línea central, o si 10 de 11 puntos consecutivos están a un lado
de la línea central, o 12 de 14, o 16 de 20. La experiencia demuestra que
cuando ocurre alguna de estas rachas, existe una causa asignable que la
produce.
·
Tendencia: si hay 6 puntos consecutivos
ascendentes o descendentes. La experiencia demuestra que cuando ocurre una
tendencia, existe una causa asignable que la produce.
·
Acercamiento a los límites de
control: si 2
de 3 puntos consecutivos está comprendidos entre 2s y 3s. Considerando que los datos se
distribuyen normalmente, se espera que el 4,29 % de estos estén comprendidos
entre 2s y
3s;
por lo tanto, es muy poco probable que 2 de 3 puntos consecutivos estén en
dicho rango, salvo que exista una causa asignable.
·
Acercamiento a la línea central: si la gran mayoría de los
puntos están entre –1s y +1s. Esto se debe generalmente a
que las muestras se han tomado en forma inapropiada, ya que es poco probable
que el proceso haya mejorado tan rápidamente.
·
Periodicidad: si hay tendencia ascendente y
descendente de forma consecutiva, para casi el mismo intervalo.
Es importante recordar que para
cualquier variable aleatoria que siga una distribución normal:
·
El
68,26% de la población está comprendida entre -1s y +1s.
·
El
95,44% de la población está comprendida entre-2s y +2s.
·
El
99,73% de la población está comprendida entre -3s y +3s.
En la Figura 6 se pueden apreciar las 6 franjas que hay entre la línea central ± 3s. Si un gráfico de control de
una medida que se distribuye normalmente consta de 20 puntos, se espera, aproximadamente:
·
Que
haya 14 puntos entre -1s y +1s.
·
Que
haya 19 puntos entre -2s y +2s.
·
Que
haya 1 punto más allá de -2s y de +2s.
Evidentemente
estas cantidades esperadas son aproximadas, y se debe tener cierta flexibilidad
para juzgar si la variable se distribuye normalmente o no.
Instalación de un gráfico de control
Una vez que ya se ha decidido qué tipo de gráfico se va a
trazar para controlar un proceso, se requiere tomar una serie de muestras,
anotar los datos y calcular la medida central y los límites de control. Estos
tres valores que se determinen, es decir, la medida central o media, el límite
de control superior y el límite de control inferior, servirán para controlar el
proceso durante un buen tiempo, hasta que dicho proceso cambie o mejore
considerablemente; cuando esto ocurra, será necesario recalcular la media y los
límites de control, pues ya serían obsoletos.
Una vez que se han determinado la media y los límites de
control, se puede verificar si el proceso está bajo control, es decir, si no
hay ningún punto fuera de los límites de control, ni una racha, tendencia,
acercamiento a los límites, acercamiento a la media o periodicidad. Si así
fuera, se aceptan la media y los límites, y ya se puede decir que el gráfico de
control ha sido instalado. En caso contrario se deben buscar las causas
asignables que han deformado el proceso, ya que está fuera de control, y
corregirlo. Una vez que se hagan las correcciones oportunas, se intentará
nuevamente instalar el gráfico de control, tomando otra serie de muestras.
Recuérdese que, si hay un punto fuera de los límites de
control, es probable (0,0027) que no se deba a una causa asignable.
Si uno o dos puntos del gráfico
están fuera de los límites de control, se pueden eliminan dichos puntos y
recalcular la medida central y los límites de control. Esto tiene una
explicación: si durante 20 o más momentos el proceso se ha salido de control
solo en dos ocasiones, valdría la pena obviar esa ocasión o esas dos ocasiones,
considerando que no ha perturbado el proceso en general. Si después de esto,
los puntos restantes quedan dentro de los límites de control, se puede instalar
el gráfico de control; en caso contrario, se deben buscar las causas asignables
que deformaron el proceso y tratar de corregirlo. Una vez que se hagan las
correcciones oportunas, se intentará nuevamente instalar el gráfico de control;
para esto, se vuelve a tomar otra serie de muestras.
Si tres o más puntos están fuera de
los límites de control, se deben buscar las causas asignables que han deformado
el proceso, ya que está fuera de control, y tratar de corregirlo. Una vez que
se hagan las correcciones oportunas, se intentará nuevamente instalar el
gráfico de control, tomando otra serie de muestras.
Asimismo, si en el gráfico se
encuentra una racha, tendencia, acercamiento a los límites, acercamiento a la
media o periodicidad, se deben buscar las causas asignables que han deformado
el proceso, ya que está fuera de control, y se debe proceder a corregirlo. Una
vez que se hagan las correcciones oportunas, se intentará nuevamente instalar
el gráfico de control, tomando otra serie de muestras.
Cabe resaltar que si, en el intento de
instalar un gráfico de control de medias, se presenta un acercamiento a la
línea central (la gran mayoría de los puntos están entre –1s y +1s), lo más probable es que las
desviaciones estándar dentro de las muestras sean muy grandes, y por lo tanto
resulte muy grande. Esto estaría ocasionando que los límites de
control resulten muy lejanos a los valores graficados, pues
.
Qué implica
que un proceso esté bajo control
Si un proceso está bajo control,
no necesariamente hace lo que supuestamente tiene que hacer. Que esté bajo
control significa que el proceso está funcionando bien, que no hay causas
asignables que lo deformen y que está en condiciones de dar un producto o
servicio consistente, de acuerdo a sus posibilidades.
Cuando un proceso esté bajo control,
recién conviene determinar qué tan capaz es de cumplir las especificaciones que
tenga. Si no lo está, no se tendrá una medida correcta de su verdadera
capacidad.
NOTA: en los próximos artículos iré publicando algunas aplicaciones.
Tabla de coeficientes para calcular los límites de control de los gráficos de control de variables:
NOTA: en los próximos artículos iré publicando algunas aplicaciones.








Comentarios
Publicar un comentario