1. Definición de función de probabilidad
Una función de probabilidad (f. de p.)
de una variable aleatoria discreta X, se define como el conjunto de
parejas ordenadas {xi, f(xi)}, donde
xi representa un valor que puede tomar X, y f(xi)
es la probabilidad de que X asuma dicho valor, de tal forma que ∑ f(xi) = 1.
Se le suele llamar distribución de probabilidad a dicho conjunto de parejas, y función
de probabilidad a la función f(x), la cual asigna las probabilidades a
los valores que puede tomar X.
Ejemplo 1:
Un experimento consiste en
lanzar un dado, cargado de manera que la probabilidad de ocurrencia de cada
cara es proporcional al número de puntos que tiene. Si se define X como
el resultado de un lanzamiento, se deduce que:
De manera que:
Ejemplo 2:
Se lanzan dos monedas. Si se define X como el número de caras que se obtiene en un lanzamiento, no hay forma de expresar f(x) como en el ejemplo anterior; la función de probabilidad se expresa simplemente con la tabla:
La f. de p. se suele representar gráficamente con diagramas de barras, tal como la distribución de frecuencias no agrupadas
Ejemplo 3:
Se quiere determinar la distribución de probabilidad del número de pacientes que llegan a una clínica dental en un intervalo de una hora. En primer lugar, se debe tomar datos del número de pacientes que llegan a la clínica dental, en varios intervalos de una hora, durante varios días. Supóngase que se obtienen los siguientes resultados:
 |
En segundo lugar, se construye una tabla de distribución de frecuencias:
Finalmente, se estiman las probabilidades “experimentales” f(x), dividiendo cada frecuencia entre la suma de frecuencias, que es 80, resultando:
Lógicamente, estas probabilidades experimentales serán más certeras mientras mayor sea el número de veces que se repite el experimento, es decir, mientras más datos se tomen del número de pacientes que llegan a la clínica en un intervalo de una hora.
2. La función de distribución (acumulativa)
La función de distribución, F(x), acumula en forma sucesiva las probabilidades f(x) de la siguiente forma: si los posibles valores que puede tomar X, ordenados en forma ascendente, son: x1, x2, x3, ... , xn.
Entonces:
F(x1) = f(x1)
F(x2) = f(x1) + f(x2)
F(x3) = f(x1) + f(x2) + f(x3)
...
F(xn) = f(x1) + f(x2) + f(x3) + ... + f(xn) = 1
El conjunto de parejas de valores {x ,F(x)} se suele expresar en una tabla, tal como la f.de p., y gráficamente en forma escalonada, tal como la distribución de frecuencias acumulativas no agrupadas.
3. El valor esperado de una variable aleatoria discreta
Se ha visto que la media aritmética de un conjunto de n datos se calcula mediante la expresión:
Cuando n tiende a ser un valor muy grande, fi / n puede sustituirse por la probabilidad f(x), ya que representa una probabilidad experimental, tal como se vio en el primer capítulo. Así, dicha media aritmética representa la media de la población o el valor esperado de la variable aleatoria X.
Por lo tanto, dada una variable aleatoria con f.de p. {x, f(x)}, la media aritmética teórica o valor esperado de X es:
Si un experimento se repite indefinidamente y se anotan los resultados que se van obteniendo; es decir, los valores que va tomando la variable aleatoria X, la media aritmética de estos tenderá a 𝝻.
Ejemplo 1:
Se lanza un dado normal. ¿Cuál es el valor esperado?
Conocida la función de probabilidad, se calcula:
µ = 1(1/6) + 2(1/6) + 3(1/6) + 4(1/6) + 5(1/6) + 6(1/6) = 3,5
Se entiende que, si un dado se lanza varias veces, la media de los resultados que se van obteniendo se aproxima cada vez más a 3,5. Entonces, cuando el número de lanzamientos tienda a infinito, la media de los resultados tenderá a 3,5.
Ejemplo 2:
En un juego de azar, el jugador participante debe escoger aleatoriamente tres esferas de una urna que contiene nueve esferas numeradas del 1 al 9. Si los tres números son consecutivos, el jugador ganará $2. Si sólo dos números son consecutivos, ganará $4. Si no obtiene números consecutivos perderá $6. ¿Cuál es la ganancia o pérdida esperada?
P(3 consec.) = 7/C(9,3) = 1/12
P(2 consec.) =
P(no consec.) = 1 – 1/12 – 1/2 = 5/12
La f. de p. correspondiente será:
|
x |
2 |
4 |
– 6 |
|
f(x) |
1/12 |
1/2 |
5/12 |
Y el valor esperado será m = 2(1/12) + 4(1/2) + (–6)(5/12) = – 0,333, que representa la ganancia esperada.
No sería correcto concluir que un jugador espera perder $0,33 si participa en este juego una vez, pues él ganará $2 o $4, o perderá $6; pero si juega muchas veces, en promedio perderá $0,33 por juego.
Ejemplo 3:
¿Cuántos pacientes se espera que lleguen a la clínica dental (ejemplo 3 del apartado 1) en un intervalo de una hora?
El valor esperado será: 𝝻 = 0(0,1125) + 1(0,3000) + … + 7(0,0125) = 2,013 pacientes.
Se ve claramente que, aunque el número de pacientes que llegue a la clínica dental en un intervalo de una hora, puede ser 0, 1, 2, … etc., es correcto afirmar que el número esperado de pacientes que llegan es 2,013, interpretándose este valor como un promedio. Por lo tanto, no tiene sentido redondear dicho valor, argumentando que se trata de una variable aleatoria discreta.
4. Varianza y desviación estándar de una variable aleatoria discreta
A partir de la definición de varianza muestral, se deduce fácilmente la varianza de una variable aleatoria, con f. de p. conocida:
Cuando n tiende a ser un valor muy grande, fi / n puede sustituirse por la probabilidad f(x), ya que representa una probabilidad experimental, y la media muestral (x̅
La desviación estándar es la raíz cuadrada positiva de la varianza.
Ejemplo:
Determine la desviación estándar del número de pacientes que llegan a la clínica dental del problema anterior.
s 2 = 0,1125(0)2 + 0,3000(1)2 + 0,2125(2)2 + … + 0,0125(7)2 – (2,013)2 = 3,825
s = 1,956
Generalmente el valor numérico de la desviación estándar de una variable aleatoria, por sí solo, no da información de qué tan dispersos están los valores que tome dicha variable aleatoria, salvo que esta tenga una distribución normal. Sin embargo, puede ser útil para compararlo con el valor numérico de la desviación estándar de otra muestra.
5. Teoremas sobre el valor esperado y la varianza
Definida una variable aleatoria X, se deducen el valor esperado y la varianza de una función h(X):
Se deducen además seis teoremas, que se presentan a continuación con sus respectivas demostraciones:
T1. E(kX) = kE(X)
E(kX) = S f(xi)(kxi) = k Sf(xi)(xi) = kE(X)
T2. E(X+k) = E(X) + k
E(X+k) = S f(xi)(xi + k) = S f(xi)(xi) + k S f(xi) = E(X) + k
T3. E(k) = k
E(k) = S f(xi)k = k S f(xi) = k
T4. E(X – m) = 0
E(X – m) = S f(xi)(xi – m) = S f(xi)(xi) – m S f(xi) = m – m = 0
T5. s 2kX = k2 s 2X
s 2kX = S f(xi)(kxi – mkX)2 = k2 S f(xi)(xi – m x)2 = k2s 2X
T6. s 2X+a = s2X
s 2X+a = S f(xi)[(xi + a) –
m X+a]2 = S f(xi)(xi – mX)2 = s 2X
A partir de la varianza 𝞼 2 h(X) se deduce fácilmente que la varianza de X es el valor esperado del cuadrado de la desviación de la media m, es decir:
NOTA: Estos teoremas también son válidos para la media aritmética de una muestra y para la varianza de una muestra.
Ejemplo:
La calificación promedio en una prueba de Estadística fue 9,24, con una desviación estándar igual a 1,25. El profesor desea ajustar todas las calificaciones por igual, de manera que el promedio resulte 11 y la desviación estándar 2,50. ¿Qué debe hacer para conseguirlo?
Sean las variables: X, las calificaciones iniciales.
Y, las calificaciones corregidas.
Evidentemente:
sY = ksX
Entonces: 11 = 9,24k + a
2,5 = 1,25k
Resolviendo: k = 2 ; a = – 6,52
El profesor debe multiplicar cada calificación por 2, y luego restarle 6,52.
6. Distribuciones de probabilidad en Excel
Existe una herramienta de Excel que puede ayudar a interpretar correctamente la función de probabilidad. Esta herramienta genera un conjunto de números aleatorios que sigue una función de probabilidad determinada.
Ejemplo:
La demanda semanal de cierto artículo es una variable aleatoria, cuya función de probabilidad es la siguiente:
Simule la demanda de este artículo durante 400 semanas consecutivas y verifique si la demanda promedio coincide con el valor esperado de la demanda semanal
Ingresando a Datos/Análisis de datos/Generación de números aleatorios, Excel muestra un cuadro de diálogo que pide:- Número de variables: aquí se ingresa el número de columnas donde se generarán los números aleatorios.
- Cantidad de números aleatorios: aquí se ingresa la cantidad de números aleatorios que se generarán en cada columna.
- Distribución: aquí se escoge la distribución discreta.
- Rango de entrada de valores y probabilidades: aquí se ingresa el rango de celdas donde están las parejas de valores {xi, f(xi)} (en dos columnas).
A continuación se muestran los números aleatorios generados por Excel, que simulan las demandas semanales durante 400 semanas consecutivas. El promedio de estos valores es 2,278, que es bastante aproximado al valor de 𝝻 = 2,25.
A manera de ejercicio, el lector podría ingresar estos 400 datos a Excel, construir la tabla de distribución de frecuencias (con la función FRECUENCIA) y luego, dividiendo entre 400 cada una de las frecuencias, determinar la distribución de probabilidad, que debería corresponder, aproximadamente, con la distribución de probabilidad dada al inicio del problema.







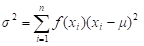



Comentarios
Publicar un comentario